Sigmoid Function Simplified

 

                          Sigmoid function Equation

Definition 

Technical Wikipedia Definition : A sigmoid function is a bounded, differentiable, real function that is defined for all real input values and has a non-negative derivative at each point and exactly one inflection point.

Simple Definition - It is basically a 'S' curve or activator function which is commonly used in Machine Learning, it is used to bound/transform/squash a wide range of values within [0,1].

Basic illustration of how Sigmoid Function works,

Defining the Input - Array containing 99999 equally spaced numbers between -10,10

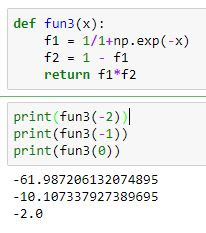
Defining the Sigmoid Function - 

Plot of the transformed values - 

Graph between input and transformed output

                                        Distplot of the Transformed values

As we can see from the above plots the values are bounded between 0,1 for any given value.

Plot if it had been e^x instead of e^-x :

Now going back to the Technical Definition,

A sigmoid function is a bounded, differentiable, real function that is defined for all real input values and has a non-negative derivative at each point and exactly one inflection point

• It has non-negative derivative at each point, the meaning of this statement is 

A Non-negative derivative means that the function is increasing, in other words increasing slope which can be seen from below figure -

• Exactly one inflection point, means point on the graph of a function at which the concavity changes.

       Point of deflection occur where the second derivative is zero, in other                   words f '' = 0 

    

The above figure shows the graph of second derivative of Sigmoid function

Upon applying second derivative and storing the respective values in a dataframe. We can see that, the inputs are the 99999 equally spaced values between [-10,10] and col_1 are the respective output values. 

    

There is exactly one ZERO value which indicates that one inflection point like mentioned in the technical definition.